Grafo lau
Grafo teorian grafo lau deritzo planoan marraztu daitekeen grafo bati, ertzak haien artean gurutzatu gabe. Alboko adibideetan K5 eta K3,3 gutxieneko grafo ez lauak dira, eta horietatik abiatuta zehaztu daitezke gainerako grafo ez-lauen ezaugarriak.
Edozein grafo lau esferaren gainean marraztu daiteke, baita alderantziz.
| Adibideak | |
|---|---|
| Grafo laua | Grafo ez-laua |
 |
 |
 |
 |
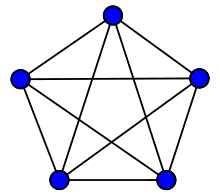Kuratowskiren Teorema aldatu
Kazimierz Kuratowski matematikari poloniarrak grafo lauen karakterizazio bat aurkitu zuen, Kuratowskiren teorema bezala ezagutzen dena.
Beste irizpide batzuk aldatu
Zaila da Kuratowskiren teorema erabiltzea grafo bat zaila den azkar erabakitzeko. Arazo hau konpontzeko algoritmo azkar bat dago: a ertz eta n erpin dituen grafo bat izanik, posiblea da grafoa laua den zehaztea Eulerren formularekin.
Eulerren formula aldatu
Eulerren formulak dio grafo lau lotu batek honakoa betetzen duela:
Grafo lau lotu batek "v" erpin, "a" ertz eta "c" aurpegi izanik, orduan
"v"-"a"+"c"=2 betetzen da
Aurreko adibideetan, lehen grafo lauan (K6-a) honako hauek ditugu: v = 6, a = 7 eta c = 3. Bigarren grafoa ertz-elkargunerik gabe marraztuz, v = 4, a = 6 eta c = 4 izango genuke, grafoa laua izanik. Ohartu Eulerren formula poliedro sinpleetarako ere baliagarria da. Ez da kasualitatea: poliedro sinple bakoitza grafo lau eta lotu gisa ikus daiteke, poliedroaren erpinak grafoaren erpin gisa erabiliz, eta poliedroaren ertzak grafoaren ertz gisa. Grafo lauaren aurpegiak edo eskualdeak poliedroaren aurpegiak dira. Adibidetakoko bigarren grafo laua, adibidez, tetraedro bati dagokio.
Beste irizpide batzuk ondoko bi teoremak dira:
1. Teorema
G grafo lau bat bada n ≥ 3 erpin dituena, orduan a ≤ 3n - 6
Hau da, n erpin dituen grafo lauak, izanik, gehienez ertz izango ditu.
| 1. Teoremaren frogapena |
| Supongamos el caso en el cual tenemos un grafo plano G triangular, es decir, un grafo con caras delimitadas por tres aristas, también llamados grafos planos maximales de v vértices, a aristas y c caras.
Demagun G grafo plano triangeluarra daukagula, hau da, hiru ertzez mugatutako aurpegiak dituen grafo bat, "v" erpin , "a" ertz eta "c" aurpegi dituena. Aurpegi bakoitza 3 ertzez mugatuta dagoenez, eta ertz bakoitza 2 aurpegiren muga denez, honakoa dugu: 3c ≤ 2a. Horrez gain, Eulerren formulatik v − a + c = 2 dela dugu, hirurekin biderkatuz 3v − 3a + 3c = 6. 3c 2a-rekin ordezkatuz 3 erpin baino gehiago dituen edozein grafo lau triangeluarra izan daitekenez ertzak gehituz, a ≤ 3v-6 dela dugu. ∎ |
2. Teorema
"n > 3 bada eta ez badago 3 luzerako ziklorik, orduan "a ≤ 2n - 4
| 2. Teoremaren frogapena |
| G grafo laua izanik, triangelurik ez duena eta v erpin, a ertz eta c aurpegi dituena:
Grafoaren aurpegiak gutxienez 4 luzerako ziklo batez egongo dira mugatuta, beraz: 2a ≥ 4c. Eulerren formulatik v − a + c = 2 dugu, laurekin biderkatuz 4v − 4a + 4c = 8 dena. 4c bakanduz "4c = 8 - 4v + 4a lortzen dugu. Adierazpen hori 2a ≥ 4c desberdintasunean ordezkatuz 2a ≥ 8 - 4v + 4a dela lortzen dugu, bakanduz: a ≤ 2v - 4 ∎ |
1 teorematik ondorioztatzen dugu K5 ez dela laua, 5 ertzeko grafo lau batek gehienez 9 ertz izan ditzakelako, baina K5-ek 10 ertz dituenez ez da laua. K3,3-ren kasuan, 6 erpin ditu eta ez du 3 luzerako ziklorik, baina 9 ertz dituenez, 2. teoremak dio ezin dela laua izan.
Ohartu teorema hauek norabide bakarreko inplikazioarekin adierazita daudela, eta ez bi norabideetan. Hori dela eta, bakarrik erabili daitezke grafo bat laua ez dela ziurtatzeko, baina ez dute frogatzen grafo bat laua denik. Bi teoremek huts egiten badute, beste metodo batzuk erabili behar dira.
Kanpo estekak aldatu
Datuak: Q547823
Multimedia: Planar graphs / Q547823
